Defi - Uniswap

区块链，目前比较火的技术之一，目前众说纷纭，各自都持有各自的看法。但接触过区块链的人或多或少
都知道 defi（Decentralised Finance)。而在 defi 中，又以 Uniswap 为代表。

Uniswap，或者叫做 CFMM (Constant Function Maket Maker)，是目前 defi 中的龙头之一。
其功能是让 Ethereum 上的不同的 token 之间自由地兑换。因为是使用的是合约实现的，加上去中心化
的属性，确保了平台的公开透明，且不易被中心化的机构操控。但既然是兑换平台，那么就可能存在套利
空间[8][9]。本文将从其设计和代码层面进行分析。Uniswap 有三个版本 V1, V2 和 其中 V1 是用
Vyper 实现的，最初的版本，token 之间的 swap 是通过 ETH 来中转的。V2 是用 solidity 实现的，
实现了不同的 ERC20 token 之间直接 swap，同时也支持 flash swap。但是 V2 版本的滑点较高，
价格区间较小，所以有了 V3，让价格区间更大了，同时可以直接追踪各个 token 的价格。

P.S. 其中参考文档中 Towards a Theory of Maximal Extractable Value I:
Constant Function Market Makers 中第 10 页中的公式：
$G(\Delta + \Delta^{sand}) - G(\Delta^{sand}) = (1 + \eta)G(\Delta)$
有误，正确的应该是：
$G(\Delta + \Delta^{sand}) - G(\Delta^{sand}) = (1 - \eta)G(\Delta)$ 。
同时公式 (2) 应该也是错的，反正我是推不出那个公式，如果是用 token B 去换 token A
的话，那么得到的 A 的数量应该是：
$\Delta’ = -\frac{R_AR_B}{R_B + \gamma\Delta} + R_A$，
如果说是 $\Delta$ 与 $\Delta’$ 的关系，那么应该是:
$G(\Delta) = \Delta = \frac{1}{\gamma}(\frac{R_AR_B}{R_A - \Delta’} - R_B)$
这个都是可以从公式 (1)：
$(R_A - \Delta’)(R_B + \gamma\Delta) = R_AR_B = K$
可以推导出来，可能是作者打错了吧。（本文的结果和其参考文档中给出的公式是一致的）

CFMM

在分析 Uniswap 前，首先要了解什么是 CFMM。其本质就一个函数[2]：

$$
x \times y = k \tag{1}
$$

其中 x, y 是对应 token 的数量，而 k 是个常数（不变），这样就能保持 token x, y
之间对应价格的稳定。所以其对应的价格为：$P(x) = \frac{x}{y}$, $P(y) = \frac{y}{x}$。
也就是说这时候要用 $\Delta$ 的 x 去兑换 y 的话，可以得到 $y - \frac{k}{x-\Delta}$
的 y。对应的价格也就变成了
$P_y(x) = \frac{y + \Delta y}{x + \Delta x},
P_x(y) = \frac{x + \Delta x}{y + \Delta y},
\Delta x = \Delta, \Delta y = y - \frac{k}{x - \Delta}$。
不管是 V1，V2 还是 V3，其最核心的公式就是这个。公式的具体分析参见{ref}appendix-a。

概述

Uniswap 其主要功能就是交互 token。就三个功能：

• Swap Tokens
• Add Liquidity
• Remove Liquidity

Swap Tokens 功能为主，大部分用户就是用的这个功能。但是这个 Swap 功能是要建立在有 Liquidity
Pool 上，需要有大户创建提供 Liquidity。既然有创建，那么也就需要有销毁咯。

V1

V1 版本很简单，就是对 $x \times y =k$ 公式的直接应用。其主要的特点是消耗的 gas 低，同时支持
ETH <-> ERC20 和 ERC20 <-> ERC20 之间的兑换[1]。

ETH <-> ERC20

用 ETH 换 ERC20 很简单，就是将对应的 ETH 转到对应的合约上，然后将对应的 ERC20 token 转回来。
计算也很简单，就是套用公式：

$$
(x + \gamma\Delta x) \times (y - \Delta y) = k = x \times y
$$

其中 x 为 ETH，y 为 ERC20，$\Delta x$ 为需要交换的 ETH，$\Delta y$ 为要换出来的 ERC20，
$\gamma = 1 - \rho$，$\rho$ 为平台的手续费，Uniswap 默认为 0.3%。即：

$$
(x \times 1000 + 997 \times \Delta x) \times (y - \Delta y) = x \times y
$$

代码为：

@private
@constant
def getInputPrice(input_amount: uint256, input_reserve: uint256, output_reserve: input256) -> uint256:
    assert input_reserve > 0 and output_reserve > 0
    input_amount_with_fee: uint256 = input_amount * 997
    numerator: uint256 = input_amount_with_fee * output_reserve
    denominator: uint256 = (input_reserve * 1000) + input_amount_with_fee
    return numerator / denominator

@private
@constant
def getOutputPrice(output_amount: uint256, input_reserve: uint256, output_reserve: uint256) -> uint256:
    assert input_reerve > 0 and output_reserve > 0
    numerator: uint256 = input_reserve * output_amount * 1000
    denominator: uint256 = (output_reserve - output_amount) * 997
    return numerator / denominator + 1

其中代码中所谓的 Price 其实是返回交换后得到对应 token 的数量，不是真正的价格。即
getInputPrice 是在给定 $x, y, \Delta x$ 的情况下返回
$\Delta y = \lfloor\frac{\alpha\gamma}{1 + \alpha\gamma} y\rfloor$ 的值。
getOutputPrice 是在给定 $x, y, \Delta y$ 的情况下返回
$\Delta x = \lfloor\frac{\beta}{1 - \beta} \cdot \frac{1}{\gamma} \cdot x\rfloor + 1$
的值。其中 $\alpha = \frac{\Delta x}{x}, \beta = \frac{\Delta y}{y},
\gamma = 1 - \rho, \rho = 0.3%$。

因此， getInputPrice 的实现的公式为：

$$
\frac{(997 \times \Delta x \times y)}{1000 \times x + 997 \times \Delta x}
$$

getOutPrice 的公式为：

$$
\frac{1000 \times x \times \Delta y}{997 \times (y - \Delta y)} + 1
$$

P.S 这里对结果进行向下取整的原因是 Vyper 中算术运算是不支持浮点数，所以就直接向下取整咯，
至于为什么 $\Delta x$ 要取整后再加 1，而 $\Delta y$ 取整后却不用加 1。个人看法是
$\Delta x$ 是用户出的，所以多出一点后的 token 会加入到流动性池中，但是 $\Delta y$ 是
从流动性池中取出来，不可能多给你，那样次数多了后容易将池子掏空。我相信你懂我的意思的。

示例：ETH -> OMG

假设 ETH/OMG 流动池中有 10 ETH 和 500 OMG。即 x = 10, y = 500, k = x _ y = 5000。
这里 ETH:OMG = 1:50，也就是 1 ETH = 50 OMG。如果有人需要将 1 ETH 换成 OMG，即
$\Delta x = 1$。则 $x’ = 10 + 0.977 = 10.977, y’ = 455.4978591600619$，
$\Delta y = y - y’ = 44.50214083993808$，即 1 ETH 最终能换到大概 44.5 OMG。
因为手续费是该流动性池中，所以新的 k 值为 11 _ 455.4978591600619 = 5010.4764507606815。
实际上是 1 ETH = 44.5 OMG，OMG/ETH 的汇率变低，如果有人还用 ETH 来换 OMG，
则 OMG/ETH 的汇率会更低，相反 ETH/OMG 的汇率就更高，这时用 OMG 换 ETH 就会更值，
所以就会有人进行套利，因此确保 ETH 和 OMG 之间的汇率保持在一个相对稳定的价格。

ERC20 <-> ERC20

由于 ETH 不是 ERC20，但是是个共用的 pair，所以可以用 ETH 来中转。所以 ERC20 和 ERC20
之间的兑换本质上还是 ETH 和 ERC20 的兑换，只不过是将两个兑换合并到了一起。例如你要用 token
ABC 来兑换 token XYZ，那么实际的操作是将 ABC 兑换成 ETH，再将 ETH 兑换成 XYZ。

实际的代码比较多，如果想了解具体实现的可以访问其 Github 地址：
https://github.com/Uniswap/v1-contracts。

一下是算法的代码：

ABC Exchange 合约代码：

contract Factory():
    def getExchange(token_addr: address) -> address: constant

contract Exchange():
    def ethToTokenTransfer(recipent: address) -> bool: modifying

factory: Factory

@public
def tokenToTokenSwap(token_addr: address, tokens_sold: uint256):
    exchange: address = self.factory.getExchange(token_addr)
    fee: uint256 = tokens_sold / 500
    invariant: uint256 = self.eth_pool * self.token_pool
    new_token_pool: uint256 = self.token_pool + tokens_sold
    new_eth_pool: uint256 = invariant / (new_token_pool - fee)
    eth_out: uint256 = self.eth_pool - new_eth_pool
    self.eth_pool = new_eth_pool
    self.token_pool = new_token_pool
    Exchange(exchange).ethToTokenTransfer(msg.sender, value=eth_out)

XYZ Exchange 合约中的代码：

@public
@payable
def ethToTokenTransfer(recipent: address):
    fee: uint256 = msg.value / 500
    invariant: uint256 = self.eth_pool * self.token_pool
    new_eth_pool: uint256 = self.eth_pool + msg.value
    new_token_pool: uint256 = invariant / (new_eth_pool - fee)
    tokens_out: uint256 = self.token_pool - new_token_pool
    self.eth_pool = new_eth_pool
    self.token_pool = new_token_pool
    self.invariant = new_eth_pool * new_token_pool
    self.token.transfer(recipent, tokens_out)

ABC 兑换 XYZ 的调用顺序是： ABC Exchange 合约中的 tokenToTokenSwap，再其中计算 ABC
对应 ETH，然后 ETH 的数量和调用者的地址传给 XYZ Exchange 合约中的 ethTokenTransfer，
将 ETH 换成 XYZ，然后再将得到的 XYZ 发送给调用者。

至于添加流动性池和销毁流动性池，这个也没什么，按照提供的流动性所占的比例分发平台币给你，然后那个
平台币就是之后赎回（销毁）流动性池的凭证，同时这些平台币的占比也是后续交易手续费的分成占比。

总结

对于 V1 版本的 Uniswap 来说，做的比较粗糙。

1. ERC20 与 ERC20 之间的兑换中转了一下，这里多花了一笔 gas fee，同时如果抽取手续费的话，
   中间的损耗会更大。
2. 价格很容易被操控，比如说其他的合约调用了其价格进行操作，这时的价格就会波动，套利者就可以
   进行套利。或者更甚的是攻击者可以直接进行砸盘操作，直接将池子掏空。

V2

V2 版本与 V1 相比，增加了以下新的特性。

• ERC20 的 pair
• 价格预言机（Price Oracle）
• Flash Swap
• 平台手续费可开关
• 流动性池之间的元交易

ERC20 Pairs

x * y = k 模型有两个无法避免的缺陷，其中一个就是会有无常损失。由 Appendix-c 可知，每次价格
波动时，就会有套利，每次兑换都会导致 LP （Liquidity Provider）的资产出现无常损失。而在 V1
版本中，不同的 ERC20 之间的兑换是通过 ETH 进行中转的，这样就会将无常损失进一步的扩大（ABC 兑
ETH 中有一次损失，ETH 再兑 XYZ 又有一次损失）。同时，对于用户来说，每次 ERC20 的兑换都要中转，
中间的磨损（手续费，gas 费）也比较大。因此 V2 版本直接实现了 ERC20 Pair，让不同的 ERC20
之间不通过 ETH 直接兑换。这样就将 LP 的无常损失和用户的兑换成本降低一倍了。

对于套利者来说，V2 版本的套利要比 V1 版本的难。因为 V1 版本有 ETH 中转，不需要计算 token
之间兑换的路径，而对于 V2 版本来说，套利者就需要通过算法来计算不同 token 之间的路径以获得
最佳套利空间，算法差的就会被算法好的进行一次套利，所以一次交易可能包含多个套利在其中。

Price Oracle

对于两个不同价值的资产（A，B），其相对价格（B 相对于 A）：$P_A(B) = \frac{R_A}{R_B}$，
其中 $R_A$ 表示 token A 的数量，$R_B$ 表示 token B 的数量。虽然中间有手续费，但是还是
可以将这个结果看作一个近似的价格，所以可以将这个值记录在链上来表示价格随时间的变化。V1 版本
不可以这么做是因为这个值太容易被人操控，而 V2 是通过时间线来记录价格，这样的话这个价格就不会
像 V1 那么容易被操控。而且 V2 版本不是记录上一次的价格，而是将每次的价格都进行累加，要计算
一个周期内的价格时：

$$
P_{t_1,t_2} = \frac{\Sigma^{t_2}_{i=t_1} P_i}{t_2 - t_1} =
\frac{\Sigma^{t_2}_{i=1}P_i - \Sigma^{t_1}{i=1}P_i}{t_2 - t_1}
$$

其中 $t_1 < t_2$，令

$$
a_t = \sum_{i=1}^n P_i
$$

则有：

$$
P_{t_1, t_2} = \frac{a_{t_2} - a_{t_1}}{t_2 - t_1}
$$

因为 $P_B(A)$（A 相对于 B 的价格）和 $P_A(B)$（B 相对于 A 的价格）的通过公式计算的结果
不能保持其乘积为 1，所以 V2 版本会同时记录下这两个价格。

其中存在一个问题就是如果有人不调用 Uniswap 的合约，而是直接给对应的 ERC20 pair 合约
转入对应的 token，这样就可以操控对应的价格了。这点的话 Uniswap 是每次 swap 后都会将
对应的 token 数量记录下来，如果当前的 token 数量和上次记录的不一致，那么就使用上次记录
下来的值进行计算。为了给一些误操作的人一些机会，Uniswap 保留了个函数 skim 可以让意外
转给合约的人将 token 提出来，同时也有一个防治有人恶意攻击时强制同步价格的函数 update：

function skim(address to) external lock {
    address _token0 = token0; // gas savings
    address _token1 = token1; // gas savings
    _safeTransfer(_token0, to, IERC20(_token0).balanceOf(address(this)).sub(reserve0));
    _safeTransfer(_token1, to, IERC20(_token1).balanceOf(address(this)).sub(reserve1));
}

function sync() external lock {
    _update(IERC20(token0).balanceOf(address(this)), IERC20(token1).balanceOf(address(this)), reserve0, reserve1);
}

又因为 Solidity 不支持浮点计算，V2 版本为了支持浮点计算，将整数部分和小数部分分开存放
然后计算，改计算库为 UQ112x112.sol。使用 112 bit 分别存储整数部分和小数部分，同时
为了更有效地利用存储，剩下的 32 bit 用来保存对应 $a_t$ 的值，即价格的累加和。

P.S 在 Solidity 中，默认整型是 uint256，即 256 bit。因为浮点数是 112 + 112 =
224 bit（uint224)，剩余 256 - 224 = 32 bit。关于 Solidity 中整型的详细介绍，
参考其官方文档：https://docs.soliditylang.org/en/latest/types.html#integers

所以 V2 版本支持的浮点数范围为 $[0, 2^{112} - 1]$，精度为 $\frac{1}{2^{112}}$，
因为 uinx 的 timestamp 也是 32 bit，即 $2^{32} - 1$ 秒，即在 Jul 02, 2106 这一天
会溢出，而 Uniswap 的是在创建后 $\frac{2^{32} - 1}{365 \times 24 \times 60 \times
60} \approx 136$ 年后才会溢出，在 2106 年后，所以在 $a_t$ 溢出前时间已经溢出了，所以这个
溢出是安全的。

同时，为了防止流动性池被掏空，Uniswap 在创建 ERC20 pair 的流动性池时，会将 10^3 个单位
token 转给 0 地址（相当于销毁）。这样就相当于只要流动性池创建，那么这个池子就会一直存在，
不会被掏空（防止出现除零问题）。

P.S 在 Ethereum 体系中，ETH 的最小单位为 wei，$1 ETH = 10^18 wei$。所以对于
销毁 $10^3$ 个单位的 token，可以忽略不计。

Flash Swaps

Flash Swaps，翻译叫做“闪电换”。何谓”闪电换”呢？在 V1 的版本中，你要兑换 token 只能先将手中的
token 转给合约，然后合约再将你需要的 token 转给你，这就意味着你在兑换之前首先需要持有 token。
而”闪电换“是在你将手中的 token 转给合约前就将你需要的 token 转给你，如果你支付的 token 数量
不对，那么这比交易会被回退，如果数量正确，则交易不变，这就是“闪电换”。通俗点说，就是你在发起兑换
时，你就会收到需要兑换的 token。为什么要有”闪电换“呢？因为有“闪电贷”啊，这种带“闪电”的，都是
快进快出的，只需要保证交易是在一个 trasaction 中完成就可以。这样对那些套利者就更友好，他们可以
实现“零元购”来进行套利，这样就会有更多的人套利，从而让价格更快的达到市场上的价格。一个经典的实例
就是 mevalphaleak.eth 实现的“零元购”：0x0efe3832b85e610fc4ba815f2be3943036a1a1be33cbd8f378a20d20667c1b39

该操作就是用到了“闪电贷”（dxdy）和“闪电换”（uniswap）。

因为有 flash swap，所以 $\Delta x$ 不是由用户提供的，而是由公式计算得出，所以就由原来的 ：

$$
(x_1 - 0.003 \cdot x_{in}) \cdot y_1 \geq x_0 \cdot y_0
$$

变成了：

$$
(x_1 - 0.003 \cdot x_{in}) \cdot (y_1 - 0.003 \cdot y_{in}) \geq x_0 \cdot y_0
$$

为了方便合约中计算，等式两边放大 1,000,000 倍，有：

$$
(1000 \cdot x_1 - 3 \cdot x_{in})\cdot(1000 \cdot y_1 - 3 \cdot y_{in}) \geq
1000000 \cdot x_0 \cdot y_0sc
$$

合约代码：

• v2-core/UniswapV2Pair.sol

function swap(
    uint256 amount0Out,
    uint256 amount1Out,
    address to,
    bytes calldata data
) external lock {
    require(amount0Out > 0 || amount1Out > 0, 'UniswapV2: INSUFFICIENT_OUTPUT_AMOUNT');
    (uint112 _reserve0, uint112 _reserve1, ) = getReserves(); // gas savings
    require(amount0Out < _reserve0 && amount1Out < _reserve1, 'UniswapV2: INSUFFICIENT_LIQUIDITY');

    uint256 balance0;
    uint256 balance1;
    {
        // scope for _token{0,1}, avoids stack too deep errors
        address _token0 = token0;
        address _token1 = token1;
        require(to != _token0 && to != _token1, 'UniswapV2: INVALID_TO');
        if (amount0Out > 0) _safeTransfer(_token0, to, amount0Out); // optimistically transfer tokens
        if (amount1Out > 0) _safeTransfer(_token1, to, amount1Out); // optimistically transfer tokens
        if (data.length > 0) IUniswapV2Callee(to).uniswapV2Call(msg.sender, amount0Out, amount1Out, data);
        balance0 = IERC20(_token0).balanceOf(address(this));
        balance1 = IERC20(_token1).balanceOf(address(this));
    }
    uint256 amount0In = balance0 > _reserve0 - amount0Out ? balance0 - (_reserve0 - amount0Out) : 0;
    uint256 amount1In = balance1 > _reserve1 - amount1Out ? balance1 - (_reserve1 - amount1Out) : 0;
    require(amount0In > 0 || amount1In > 0, 'UniswapV2: INSUFFICIENT_INPUT_AMOUNT');
    {
        // scope for reserve{0,1}Adjusted, avoids stack too deep errors
        uint256 balance0Adjusted = balance0.mul(1000).sub(amount0In.mul(3));
        uint256 balance1Adjusted = balance1.mul(1000).sub(amount1In.mul(3));
        require(
            balance0Adjusted.mul(balance1Adjusted) >= uint256(_reserve0).mul(_reserve1).mul(1000**2),
            'UniswapV2: K'
        );
    }

    _update(balance0, balance1, _reserve0, _reserve1);
    emit Swap(msg.sender, amount0In, amount1In, amount0Out, amount1Out, to);
}

• v2-periphery/UniswapV2Router02.sol

function _swap(uint[] memory amounts, address[] memory path, address _to) internal virtual {
    for (uint i; i < path.length - 1; i++) {
        (address input, address output) = (path[i], path[i + 1]);
        (address token0,) = UniswapV2Library.sortTokens(input, output);
        uint amountOut = amounts[i + 1];
        (uint amount0Out, uint amount1Out) = input == token0 ? (uint(0), amountOut) : (amountOut, uint(0));
        address to = i < path.length - 2 ? UniswapV2Library.pairFor(factory, output, path[i + 2]) : _to;
        IUniswapV2Pair(UniswapV2Library.pairFor(factory, input, output)).swap(
            amount0Out, amount1Out, to, new bytes(0)
        );
    }
}

从代码中可以看出 v2-core/UniswapV2Pair.sol 中的 swap 被
v2-periphery/UniswapV2Router02.sol 中的 _swap 调用。其中 amount0In 和
amount1In 是根据 amount0Out 和 amount1out 得来的，而 amount0Out 和
amount1Out 是根据 input 的地址来进行判断计算的，所以不能确定是到底是用 x 来换 y 还是
y 换 x，为了确保流动性 k 不会减少，就就调整为了

$$
(1000 \cdot x_1 - 3 \cdot x_{in}) \cdot (1000 \cdot y_1 - 3 \cdot y_{in}) \geq
x_0 \cdot y_0
$$

Protocol Fee

在 V1 版本中，所有的手续费时转入到合约中，之后将其分发给 LPs（Liquidity Providers）。
在 V2 中，增加了一个控制手续费的开关，可以控制平台是否对手续费进行抽成，抽成为 5
个基点(0.05%)。对于整个手续费来说，平台抽成占到了 1/6 （0.05% / 0.3% = 1 / 6），
默认平台不抽成。如果平台进行抽成的话，那么每笔交易都需要多执行一次转账，而转账需要
gas fee，为了降低这部分 gas fee，平台将每次的手续费都进行累加，只有 LPs 对流动
性池进行操作是，才会对当前的手续费进行结算。

手续费的抽取是抽取 $\Delta x$ 的 0.3%，所以其增长速度是 $\sqrt k$ （$k = x \cdot y$）。
所以从 $t_1$ 到 $t_2$ 之间抽取的费用在 $t_2$ 时占流动性池的比为：

$$
f_{1,2} = \frac{\sqrt{k_2} - \sqrt{k_1}}{\sqrt{k_2}} = 1 -
\frac{\sqrt{k_1}}{\sqrt{k_2}} \tag {2}
$$

因此平台抽成在 $t_1$ 到 $t_2$ 中占流动性的比为 $\phi \cdot f_{1,2}$，其中
$\phi = \frac{1}{6}$。设 $s_m$ 为发送的流动性币（UNI），则：

$$
\frac{s_m}{s_m + s_1} = \phi \cdot f_{1, 2} \tag {3}
$$

将 $(2)$ 代入 $(3)$ 中有：

$$
s_m = \frac{\sqrt{k_2} - \sqrt{k_1}}{(\frac{1}{\phi} - 1) \cdot \sqrt{k_2} +
\sqrt{k_1}} \cdot s_1 \tag {4}
$$

将 $\phi = \frac{1}{6}$ 代入 $(4)$ 中有：

$$
s_m = \frac{\sqrt{k_2} - \sqrt{k_1}}{5 \cdot \sqrt{k_2} + \sqrt{k_1}} \cdot s_1
$$

P.S Uniswap 中流动性币为 UNI，代表提供的流动性的 share。该 share 用来计算手续费的分成。

假设提供 100 DAI 和 1 ETH 得到 10 个 share，即 10 UNI，当提供的值变为了 96 DAI 和 1.5
ETH 时，平台得到的 UNI 为（假设在提供时平台抽取已经开启）：

$$
s_m = \frac{\sqrt{96 \cdot 1.5} - \sqrt{100 \cdot 1}}{5 \cdot \sqrt{96 \cdot
1.5} + \sqrt{100 \cdot 1}} \cdot 10 \approx 0.0286
$$

所以此时平台的分成就为 0.0286 UNI。

Meta Transactions for Liduidity Pool

正常的交易中，需要支付该条链的原生代币（ETH）作为 gas fee，而 Uniswap 的代币 UNI 是 ERC20，
但是其中增加了一个函数 permit，该函数遵循 EIP712[12]，
可以让 UNI 的持有者在链下对 trasaction 进行签名，可以让其他拥有 ETH 的地址转走 UNI 持有者
中的 UNI，即可让其他地址代替自己操作 UNI。通俗点就是权益转让。因为拥有 UNI 的话就可以直接去
销毁对应的流动性。

function permit(address owner, address spender, uint value, uint deadline, uint8 v, bytes32 r, bytes32 s) external {
    require(deadline >= block.timestamp, 'UniswapV2: EXPIRED');
    bytes32 digest = keccak256(
        abi.encodePacked(
            '\x19\x01',
            DOMAIN_SEPARATOR,
            keccak256(abi.encode(PERMIT_TYPEHASH, owner, spender, value, nonces[owner]++, deadline))
        )
    );
    address recoveredAddress = ecrecover(digest, v, r, s);
    require(recoveredAddress != address(0) && recoveredAddress == owner, 'UniswapV2: INVALID_SIGNATURE');
    _approve(owner, spender, value);
}

从代码中可以看出，permit 其实就是个变种的 approve。

详细的代码分析可参考 UNISWAP CONTRACT WALK-THROUGH[2]。

总结

总的来说，V2 版本相对于 V1 版本来说，改动很大，同时这些新增的特性对于 CFMM 来说更加有利，
尤其是其 Flash Swap 和 ERC20 Pairs。让更多的人参加套利来保持其内部价格和市场价格一致。当然，
缺点也很明显，就是滑点比较高。

V3

从 V1 到 V2，改进确实很大，所以 V2 版本是使用的最多的一个版本，同时也是最受套利者们欢迎的。
但是不得不承认，V2 版本的滑点依旧是存在，为了改进这一缺陷，其他的 Defi 平台就采用了其他的
公式[10]，而 Uniswap 对 $ x \times y = k$ 这个公式进行改进，升级到 V3 版本。

V3 版本主要更新了以下几个特性：

• 集中流动性（Liquidity）
• 弹性费用
• 平台手自治
• 优化 Oracle

集中流动性

$$
\begin{align}
&L^2 = k \\
&(x + x_{offset}) \cdot (y + y_{offset}) = L^2
\end{align}
$$

由此有：

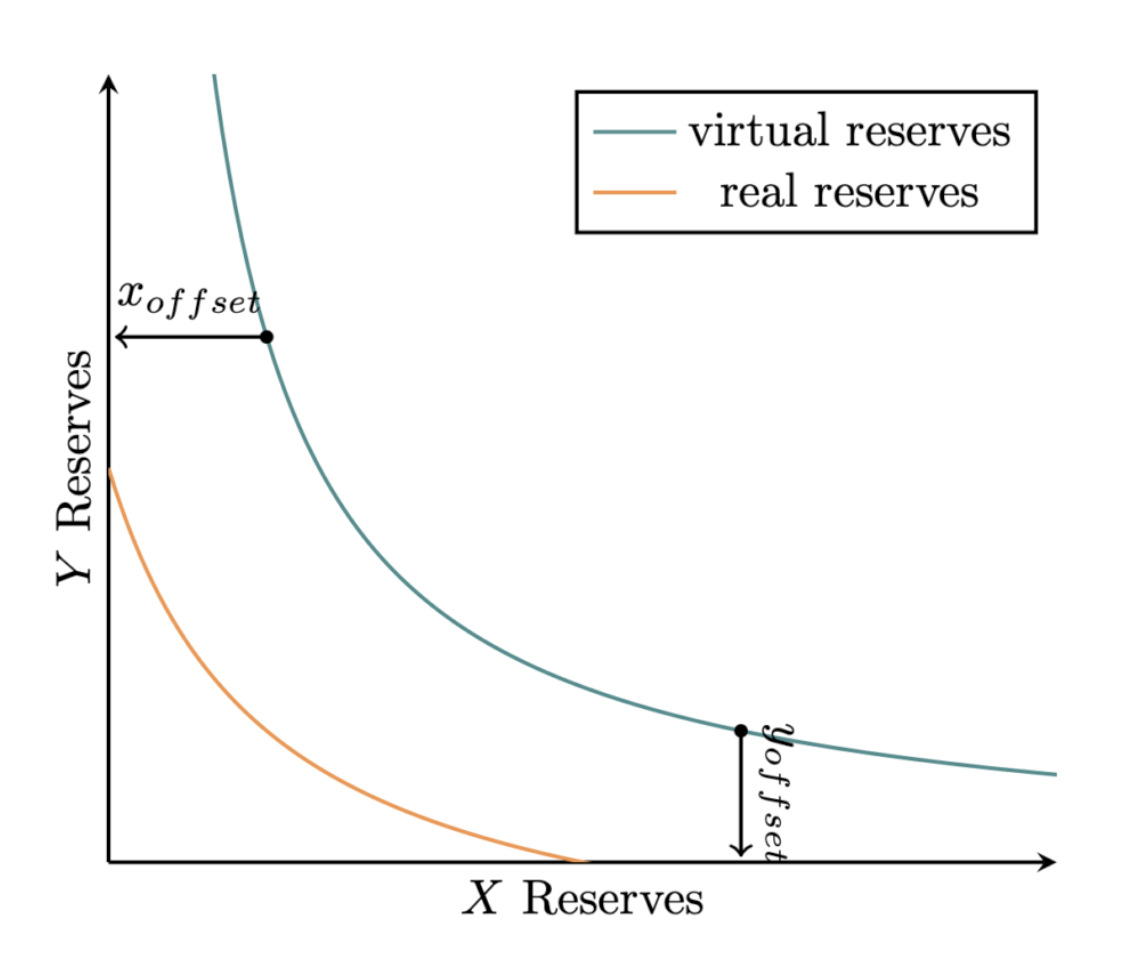
如上图所示，如果由流动性（L）来代替原来的常量（k），那么曲线就往原点方向平移了，价格区间也就由
原来的 $(0, \infty)$ 变成了一个有上下界的闭区间。设 P 为 x 相对于 y 的价格，即 $P =
\frac{y}{x}$ 则 real reserves 与 Y Reserves 轴的交点即为此前流动性价格上界的平方根，
与 X Reserves 轴的交点为当前流动性价格下界的平方根，即当前流动性的价格区间为
$[\sqrt{P_{lower}}, \sqrt{P_{uppper}}]$。因此流动性离散地分布在不同的价格区间，使用上述
公式不能恰当地描述流动性和 token 数量的关系，需要基于上述公式推导出一更恰当的公式。参照
Appendix-d，有：

$$
L = \frac{dy}{d\sqrt{P}}
$$

将每个价格区间算作一个 tick，则流动性在不同的 tick 的 分布图为：

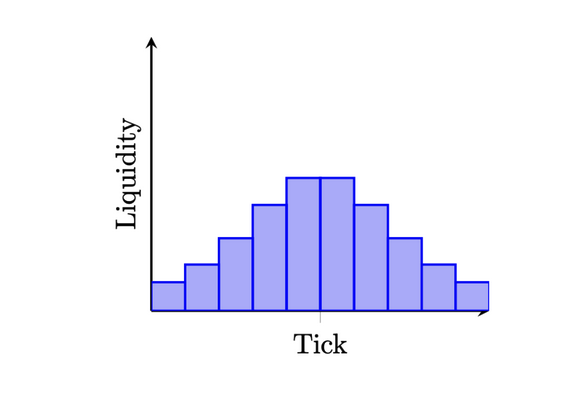
P.S 这个分布图很 poisson。

而 v2 版本对应的分布为：

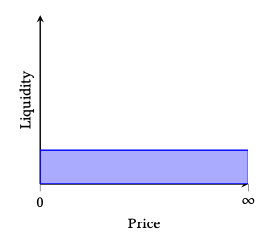
因为 Liquidity 分布不同，所以之前的用 ERC20（UNI）来作为 share 就不合适了，将其变成
ERC721 更为合适，每对 Pair 不同价格区间都有一个 ERC721，这样同时也解决了 V2 版本将手续费
存入流动性池的缺陷，V3 版本可以将手续费直接转给该流动性的 ERC721，同时平台的抽成也可以让用户
自己设置。

不同价格区间的好处是，当价格波动超出了 $P_{upper}$，Uniswap 会自动将 x 清算成 y，然后这个
价格区间就 deactive 了，当价格波动回到这个区间，Uniswap 又会自动买回 x，激活这个价格区间。
这样的话 LP 们的收益就会更大，而且无常损失也比 V2 版本的要少，同时也大大提高了资产的利用率，
因为 V2 版本能利用到的流动性就是在某个价格附近，无法大部分资产都没有利用到，而 V3 版本就能将
大量的流动性都集中在正常的价格区间，一旦价格剧烈波动，那么 LP 可以将其他的价格区间的流动性取出，
投入到新的价格区间。

弹性费用

在 V1 和 V2 版本中，交易费都是 0.3%。但是因为 V3 版本的改进，不同的价格有不同的流动性池，
所以交易费也就支持在创建流动性池时选择不同的交易费，目前是有三个不同的费率，0.05%，0.30% 和
1%。

平台自治

V2 版本中，平台的手续费是由开发者指定的，而 V3 中则将平台的手续费的管理权交到了 LP 的手中，
LP 拥有流动性池的管理权，可以控制平台抽取多少手续费，范围为 0 或是交易费的 $\frac{1}{N},
4 \leq N \leq10$。同时 LP 可以将管理权转移给其他的地址。

优化 Oracle

在 V2 版本中，Price Oracle 分别记录了 x 和 y 的价格。在 V3
版本中，改用了新公式，有：

$$
\begin{align}
&L = \sqrt{x \cdot y} \\
&P = \sqrt{\frac{y}{x}}
\end{align}
$$

所以：

$$
\begin{align}
&x = \frac{L}{\sqrt{P}} \\
&y = L \cdot \sqrt{P}
\end{align}
$$

因此对 x 和 y 的数量（Reserves）可以直接通过流动性（Liquidity）和 x 相对于 y 的价格 P
的平方根求出，不需要分别记录下 x 和 y 的价格。至于为什么是 $\sqrt{P}$ 而不是 P，是因为
取根号后同样的存储能够记录更多的价格。

总结

相比于 V2 版本，V3 版本主要是对原有的公式进行了改进，从原来的 x 和 y 数量的关系变为流动性和
x 相对于 y 的价格的关系，让流动性池的分布更加合理，即将交换的滑点降低了，也提高了资金的利用率。
同时也将流动性池的管理权移交给了 LP，而不是由平台来管控，更加的去中心化。但同样是因为流动性池
分散在不同的价格区间内，套利空间就变得很小。

What’s Next?

从 2018 年到 2022 年，从最简陋的 V1 版本，到如今的 V3 版本，短短四年间，Uniswap 在 Defi
中引领潮流，目前来看，V3 版本似乎已经很完善了，那么 Uniswap 下一步该走向何方呢？是否会进一步
引入 DID 和 zk-snark？在网上看到有人推测 Uniswap 的下一步是让用户直接交易 token，而不是
通过 token 的 pair 进行兑换，这个推论很 make sense。

个人的观点是 Defi 目前来说还是由一些数学大佬在引领，未来应该是要将公式简化出来，让更多的用户和
开发者参与进来，而不是越变越复杂，这样才能创建繁荣的生态。

That’s it, happy hacking ^_^

P.S 如果在本文中发现有错误或遗漏的地方，欢迎提 issue。

Reference:

[1]. Hayden Adams. 2018. Uniswap Whitepaper. https://hackmd.io/@HaydenAdams/HJ9jLsfTz

[2]. Yi Zhang, Xiaohong Chen and Deajun Park. 2018. Formal Specification of Constant Product ($x \times y = k$) Market Maker Model and Implementation. Retrieved Aug 31. 2022 from https://raw.githubusercontent.com/runtimeverification/verified-smart-contracts/uniswap/uniswap/x-y-k.pdf

[3]. Hayden Adams, Noah Zinsmeister and Dan Robinson. 2020. Uniswap v2 Core. Retrieved Aug 28, 2022 from https://uniswap.org/whitepaper.pdf

[4]. Ori Pomerantz. 2021. UNISWAP-V2 CONTRACT WALK-THROUGH. https://ethereum.org/en/developers/tutorials/uniswap-v2-annotated-code/

[5]. Hayden Adams, Noah Zinsmeister, Moody Salem, River Keefer and Dan Robinson. 2021. Uniswap v3 Core. Retrieved Aug 28, 2022 from https://uniswap.org/whitepaper-v3.pdf

[6]. Trapdoor-Tech. May. 2021. Uniswap - Deep Dive into V3 technical white paper. https://trapdoortech.medium.com/uniswap-deep-dive-into-v3-technical-white-paper-2fe2b5c90d2)

[7]. Trapdoor-Tech. Jun. 2021. Uniswap - Deep Dive into V3’s Source Code. https://trapdoortech.medium.com/uniswap-deep-dive-into-v3s-source-code-b141c1754bae

[8]. Kshitij Kulkarni, Theo Diamandis and Tarun Chitra. 2022. Towards a Theory of Maximal Extractable Value I: Constant Function Market Makers. Retrieved Jul 23, 2022 from https://people.eecs.berkeley.edu/~ksk/files/MEV_CFMM.pdf

[9]. noxx. 2022. DEX Arbitrage, Mathematical Optimisations & Me. https://noxx.substack.com/p/dex-arbitrage-mathematical-optimisations

[10]. Dan Robinson. 2021. Uniswap V3: The Universal AMM. https://www.paradigm.xyz/2021/06/uniswap-v3-the-universal-amm

[11]. Guillermo Angeris, Tarun Chitra. 2020. Improved Price Oracles: Constant Function Market Makers. Retrieved Sep 4, 2022 from https://www.deepdyve.com/lp/arxiv/improved-price-oracles-constant-function-market-makers-xlrgVekYST?key=acm

[12]. Remco Bloemen, Leonid Logvinov, Jacob Evans. 2017. https://eips.ethereum.org/EIPS/eip-712

Appendices

Appendix A. x * y = k 模型

$$
x \times y = k \tag{a.1}
$$

使用 $\Delta x$ 的 token X 换取 $\Delta y$ 的 token Y，有:

$$
(x + \Delta x) \times (y - \Delta y) = k
$$

令 $x’ = x + \Delta x, y’ = y - \Delta y$，则有

$$
x’ \times y’ = k = x \times y \tag{a.2}
$$

令 $\alpha = \frac{\Delta x}{x}, \beta = \frac{\Delta y}{y}$，有

$$
x’ = x + \Delta x = (1 + \alpha)x, : y’ = y - \Delta y = (1 - \beta)y \tag{a.3}
$$

由 $(a.2)$ 和 $(a.3)$ 有：

$$
(1 + \alpha)x \times (1-\beta)y = x \times y
$$

因此 $\alpha$ 和 $\beta$ 之间的关系为：

$$
\alpha = \frac{\beta}{1 - \beta}, :
\beta = \frac{\alpha}{1 + \alpha} \tag{a.4}
$$

将 $(a.4)$ 代入 $(a.3)$ 有：

$$
\begin{align}
&x’ = (1 + \alpha)x = \frac{1}{1 - \beta} x \\
&y’ = \frac{1}{1 + \alpha} y = (1 - \beta) y
\end{align}
$$

且：

$$
\begin{align}
&\Delta x = \frac{\beta}{1 - \beta} x \\
&\Delta y = \frac{\alpha}{1 + \alpha} y
\end{align}
$$

以上是在平台（即 Uniswap）不抽取手续费的情况下的结果。下面，将考虑平台会抽取一定的手续费。
设手续费为 $\rho$，$0 \leq \rho < 1$（例如，Uniswap 的手续费为 0.3%，则 $\rho = 0.003$）。

令 $\gamma = 1 - \rho$，有：

$$
(x + \gamma\Delta x) \times (y - \Delta y) = k
$$

令 $\alpha = \frac{\Delta x}{x}, \beta = \frac{\Delta y}{y}$，有：

$$
x’_\rho = x + \gamma\Delta x = (1 + \gamma\alpha) x, :
y’_\rho = y - \Delta y = (1 - \beta) y \tag{a.5}
$$

因为 $x’_\rho \times y’_\rho = k$，由 $(a.1)$ 和 $(a.5)$ 有：

$$
(1 + \gamma\alpha)x \times (1 - \beta) y = x \times y
$$

即：

$$
\alpha = \frac{1}{\gamma} \cdot \frac{\beta}{1 - \beta}, :
\beta = \frac{\gamma\alpha}{1 + \gamma\alpha} \tag{a.6}
$$

将 $(a.6)$ 代入 $(a.5)$ 有：

$$
\begin{align}
&x’_\rho = (1 + \gamma\alpha) x = \frac{1 + \beta(\frac{1}{\gamma} - 1)}{1 -
\beta} x \\
&y’_\rho = \frac{1}{1 + \gamma\alpha} y = (1 - \beta) y
\end{align}
$$

即：

$$
\begin{align}
&\Delta x_\rho = \frac{\beta}{1 - \beta} \cdot \frac{1}{\gamma} \cdot x \\
&\Delta y_\rho = \frac{\gamma\alpha}{1 + \gamma\alpha} \cdot y
\end{align}
$$

因此有：

$$
\begin{align}
x’_\rho \times y’_\rho &= \frac{1 + \beta(\frac{1}{\gamma} - 1)}{1 - \beta} x
\times (1 - \beta) y \\
&= (1 + \beta(\frac{1}{\gamma} -1)) \cdot x \cdot y
\end{align}
$$

当 $\rho = 0$ （即无手续费）时，$\gamma = 1 - \rho = 1$，$x’_\rho \times y’_\rho =
x \times y$；
当 $\rho >0$ 时，$0 < \gamma < 1$，即 $\frac{1}{\gamma} > 1 \Rightarrow
\frac{1}{\gamma} - 1 > 0$，
则 $x’_\rho \times y’_\rho > x \times y$。所以在收取收取手续费时，每次兑换后都会略有通胀。

Appendix B. 滑点

滑点（Slippage），一般只预设成交价与真实成交价格的偏差。在 CFMM 中，一旦发生交易，就会产生
滑点。交易额越大，滑点越大，交易者损失也就越大。以下是滑点的分析推导。

假设交易平台不收取交易费，有：

$$
\left{
\begin{align}
&x \times y = k \\
&(x + \Delta x) \times (y - \Delta y) = k
\end{align}
\right.
$$

由此可得：

$$
\begin{align}
\Delta y &= y - \frac{x \times y}{x + \Delta x} \\
&= \frac{y \times (x + \Delta x)}{x + \Delta x} - \frac{x \times
y}{x + \Delta x} \
&= \frac{y \cdot \Delta x}{x + \Delta x}
\end{align}
$$

即在实际交易中，y 相对于 x 的价格为：

$$
\begin{align}
P’_x(y) = \frac{\Delta x}{\Delta y}
= \frac{\Delta x}{\frac{y \cdot \Delta x}{x + \Delta x}}
= \frac{x + \Delta x}{y}
\end{align}
$$

而在交易开始时，y 相对于 x 的价格为：

$$
P_x(y) = \frac{x}{y}
$$

所以滑点就产生了，为：

$$
\begin{align}
Slippage_{P_x(y)} &= P’_x(y) - P_x(y) \\
&= \frac{x + \Delta x}{y} - \frac{x}{y} \\
&= \frac{\Delta x}{y}
\end{align}
$$

由上式有，滑点与交易额（$\Delta x$）成正比，与其流动性池中的数量（y）成反比。在 y 不变的情况
下，交易额（$\Delta x$）越大，滑点就越大。

如果交易有手续费（$\rho$）的话，则由 $(a.6)$ 及其后得到的有：

$$
\frac{\Delta x_\rho}{\Delta y_\rho} = \frac{\frac{\beta}{1 - \beta} \cdot
\frac{1}{\gamma} \cdot x}{\frac{\gamma\alpha}{1 + \gamma\alpha}y} \\
$$

其中 $\gamma = 1 - \rho, \alpha = \frac{\Delta x}{x}, \beta = \frac{\Delta
y}{y}, \beta = \frac{\gamma\alpha}{1 + \gamma\alpha}$。
所以：

$$
Slippage’_{P_x(y)} = (1 - \rho)\frac{\Delta x}{y}
$$

因为 $\rho$ 也是一个确定的值，所以结论和无手续费一致。

Appendix C. 无常损失

无常损失（Impermanent Loss），是指当资产价格剧烈波动时，持有的资产净值损耗减少，就会产生暂时
性的账面损失。放到 CFMM 中就是当价格剧烈波动时，流动行池的总价值就减少。因为其价格是靠套利者来
对价格进行调节，会造成越涨越卖，越跌越买的情况，所以流动性池中的无常损失会成为永久损失。具体分析
如下：

假设 Uniswap 的 ETH/DAI 流动池中有 10 ETH 和 400 DAI，则 k = 4000，ETH 相对于 DAI
的价格为：40 DAI/ETH。若有流动性提供者提供了 2 ETH 和 80 DAI 的流动性，则该提供者的流动性
占比为 20%。当 ETH 价格突然涨到 60 DAI/ETH 时，就会有人用 DAI 来换 ETH 进行套利。

设共用了 $\Delta x$ 个 DAI 兑换了 $\Delta y$ 个 ETH 后，Uniswap 中 ETH/DAI 的值变为
1/60，则：

$$
\begin{align}
&(10 - \Delta x) \times (400 + \Delta y) = 4000 \\
&\frac{10 - \Delta x}{400 + \Delta y} = \frac{1}{60}
\end{align}
$$

解得：

$$
\begin{align}
x \approx 1.84 \\
y \approx 89.6
\end{align}
$$

即大概用了 89.6 个 DAI 兑换了 1.84 个 ETH 后，ETH/DAI = 1/60。此时 ETH/DAI 池中有
8.16 个 ETH，489.6 个 DAI。套利的价格为 $\frac{\Delta x}{\Delta y} \approx 47.41$
DAI/ETH，比池中的价格高，存在滑点，比真实价格低，即套利空间。

在套利完成后，之前的流动性提供者在池中的资产为 1.632 ETH 和 97.92 DAI，其 $\Delta x =
0.368, \Delta y = 17.92$，而按照 ETH 的现价 60 DAI/ETH 来算，当 $\Delta x = 0.368$
时，$\Delta y = 0.368 \times 60 = 22.08 \ne 17.92$，所以就产生了 22.08 - 17.92 =
4.16 个 DAI 的无常损失。

Appendix D. Liquidity

首先，有:

$$
(x + x_{offset}) \cdot (y + y_{offset}) = L^2 \tag {d.1}
$$

由 $(d.1)$ 可得：

$$
\begin{align}
x = \frac{L^2}{y + y_{offset}} - x_{offset} \\
y = \frac{L^2}{x + x_{offset}} - y_{offset}
\end{align}
$$

又：

$$
\begin{align}
&dy = y + y_{offset} = \frac{L^2}{x + x_{offset}} \\
&dx = x + x_{offset}
\end{align}
$$

所以有：

$$
P_y(x) = \frac{dy}{dx} = \frac{\frac{L^2}{x + x_{offset}}}{x + x_{offset}} =
\frac{L^2}{x + x_{offset}} \tag{d.2}
$$

一下将 $P_y(x)$ 简写成 P。由 $(d.2)$ 有：

$$
\sqrt P = \frac{L}{x + x_{offset}} = \frac{L}{\frac{L^2}{y + y_{offset}}} =
\frac{y + y_{offset}}{L} \tag {d.3}
$$

由 $(d.3)$ 有：

$$
y = L \cdot \sqrt P - y_{offset}
$$

等式两边求导有：

$$
\begin{align}
&dy = L \cdot d\sqrt P \\
\Rightarrow &L = \frac{dy}{d\sqrt P}
\end{align}
$$